大致题意
根据中序遍历序列和后序遍历序列的结果的找出二叉树从根节点到叶子节点中每个节点的总和最小值,并输出该路线的叶子节点的值。有多条路线的时候,输出叶子节点的最小值。
解题思路
二叉树基础题,虽然是基础题还是不会,这题主要是根据中序遍历和后序遍历建立二叉树
根据二叉树中序遍历和后序遍历的特点
后序遍历的最后一个值为根节点
中序遍历中根节点之前的序列为其左子树,之后的序列为其右子树
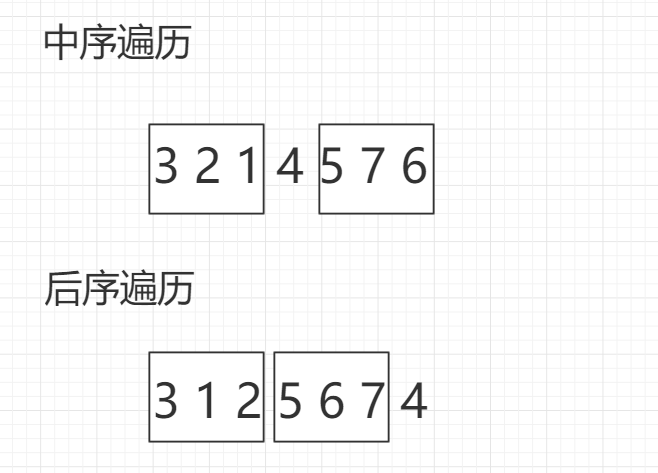
以下两个序列,可以看出4是根节点,然后中序遍历的3 2 1是其左子树,在后序遍历中,从序列起点开始同样长度的内容是即3 1 2是其左子树

根据性质可以分为
此时,再将中序遍历的左子树和后序遍历的左子树,视为根节点的中序遍历和后序遍历进行递归,只至递归至遍历序列长度为1时,即叶子节点,停止递归。
*注意:由题意得,该二叉树并非完全二叉树,即有可能存在只有左节点为空,右节点不为空情况
构建代码如下:
//in_s为中序遍历起点,in_e为中序遍历终点,post_s为后序遍历起点,post_e为后序遍历终点
void buid(int in_s, int in_e, int post_s, int post_e,Node* root) {
if (in_s > in_e) { //空树
free(root); //释放空间
root = NULL;
return;
}
if (in_s == in_e) { //叶子节点
root->value = inorder[in_s];
return;
}
int i = in_s;
root->value = postorder[post_e];
while (inorder[i] != postorder[post_e]) i++; //找到中序遍历中根节点的位置
root->left = (Node *)malloc(sizeof(Node));
root->right = (Node *)malloc(sizeof(Node));
buid(in_s, i - 1, post_s, post_s + i - in_s - 1,root->left); //建立左子树
buid(i + 1, in_e, post_s + i - in_s, post_e - 1, root->right); //建立右子树
}
这题主要是构建二叉树的问题,我本来的思路是构建二叉树之后,dfs二叉树然后再得到最小的值
但是TLE了….
所以就在构建的过程中一起计算了….
所以修改上面的代码得
//in_s为中序遍历起点,in_e为中序遍历终点,post_s为后序遍历起点,post_e为后序遍历终点,sum为当前根节点已经累加的值
void buid(int in_s, int in_e, int post_s, int post_e,Node* root,int sum) {
if (in_s > in_e) { //空树
free(root); //释放空间
root = NULL;
return;
}
if (in_s == in_e) { //叶子节点
root->value = inorder[in_s];
if (sum + root->value < _sum) { //判断是否为最小的路径
_ans = root->value;
_sum = sum + root->value;
}
if (sum + root->value == _sum) //判断多条最小路径叶子节点最小的值
_ans = min(_ans, root->value);
return;
}
int i = in_s;
root->value = postorder[post_e];
while (inorder[i++] != postorder[post_e]);i--; //找到中序遍历中根节点的位置
root->left = (Node *)malloc(sizeof(Node));
root->right = (Node *)malloc(sizeof(Node));
root->left->left = NULL; root->left->right = NULL;
root->right->left = NULL; root->right->right = NULL;
buid(in_s, i - 1, post_s, post_s + i - in_s - 1,root->left,sum + root->value); //建立左子树
buid(i + 1, in_e, post_s + i - in_s, post_e - 1, root->right, sum + root->value); //建立右子树
}